Unreal Engine 5’s “Nanite”: Looking Under the Hood
Spoiler: Don’t abandon your previous traditional rendering optimization… unless that optimization is poly count
Nanite is unreal engine’s novel solution for rendering arbitrarily dense geometry in real time. It presents developers a traditional deferred rendering pipeline with materials and meshes, but innovates by virtualizing geometry streaming so that scene complexity scales O(log(n)) with polygons instead of O(n).
Decoupling Visibility From Materials
Instead of solving this in object space, they construct a “visibility buffer” by testing for scene objects by using the current and previous frames’ HZBs (hierarchical Z-Buffers).
This “Vis Buffer” is then processed by a pixel shader that transforms the free-vertex-positions to screen space, and then derives barycentric coordinates for each pixel. With those coordinates, it then loads and interpolates vertex attributes like a typical pixel shader would. This solution:
Mitigates overdraw
Has a lot of cache hits
and has no pixel-quad inefficiencies
In conclusion, all opaque geometry can be drawn to a buffer with a single draw call, meaning that CPU cost is independent from the number of objects in the scene, or in view.
Pixel Perfect Geometry
“The cost of rendering geometry should scale with screen resolution, not scene complexity.”
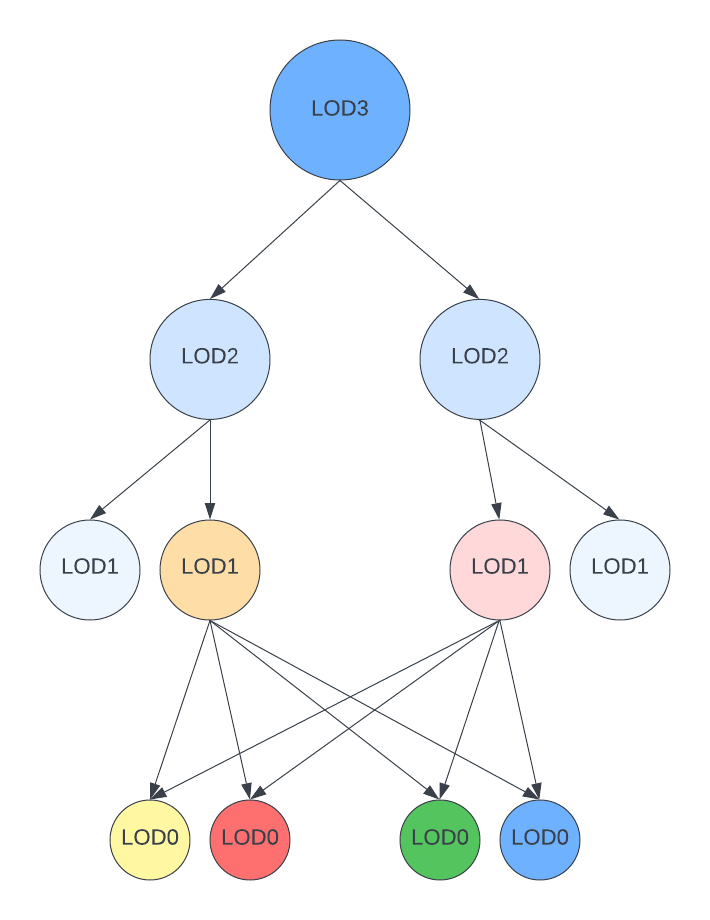
Polygon Clusters: Using the barycentric coordinates of each vertex, the renderer constructs a DAG (directed acyclic graph) of polygon clusters, where clusters combine with their neighbors to form lower (LODs) levels of details. Then, they select the LOD for each polygon-cluster using a heuristic to calculate the screen-space projected error of a cluster.
Cutting the DAG: With the DAG approach, only the cut with detail necessary for rendering the current view is needed in RAM, and the rest of the geometry data can remain in disk (hence the title “virtual geometry.” Because it’s a DAG (instead of a tree), the more shared edges there are in the graph, the less locked edges there are when simplifying poly clusters.
Because the heuristic for calculating the projected error of a cluster can reliably solve for error that’s less than a pixel, the DAG can be cut in a way that transitions between cluster LODs is imperceptible, hence the term “pixel perfect geometry.”